Trực tâm là gì? Tìm toạ độ trực tâm thế nào?
Toán hình là một phần quan trọng của môn Toán có nhiều ứng dụng trong cuộc sống. Trong chương trình lớp 7, bài toán về trực tập là gì? Tìm tọa độ trực tâm thế nào là dạng bài các bạn cần hiểu, nắm vững và biết cách vận dụng. Hãy cùng Lamsao tìm hiểu trong bài viết này nhé.
Trực tâm là gì?
Trong các bài thi, trực tâm là kiến thức được sử dụng rất nhiều. Những kiến thức sau đây sẽ giúp bạn đọc hiểu rõ hơn về các trực tâm.
Theo định nghĩa: “Trong 1 tam giác có 3 đường cao. Ba đường cao đó cùng đi qua một điểm, điểm đó chính là trực tâm của tam giác”.
Như vậy, hiểu ngắn gọn hơn chúng ta có thể hiểu như sau: Bất kỳ một tam giác nào cũng đều có 3 đường cao. Khi chúng ta cho 3 đường cao đó giao nhau thì điểm giao nhau đó chính là trực tâm.
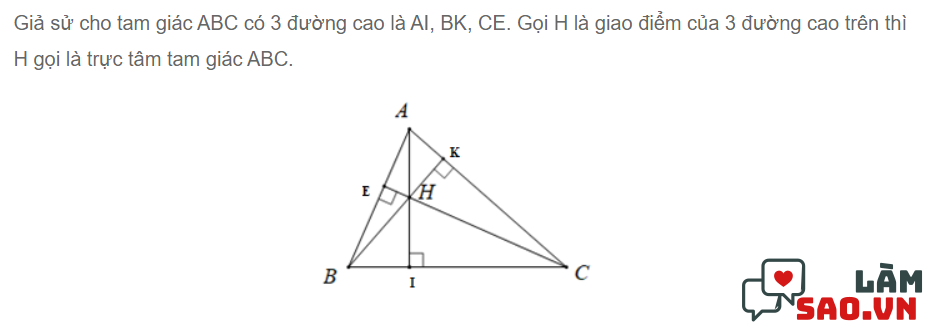
Để các bạn dễ hình dung hơn thì với hình tam giác ABC. Chúng ta sẽ kẻ 3 đường cao lần lượt xuất phát từ các đỉnh sang cạnh đối diện. Từ A kẻ AI vuông góc BC, từ B kẻ BK vuông góc AC và từ C kẻ CE vuông góc AB. Khi đó, ta sẽ có ba đường cao AI, BK và CE sẽ cắt nhau tại điểm H. Giao điểm H đó là trực tâm của tam giác ABC.
Tìm tọa độ trực tâm thế nào?
Ba đường cao của tam giác cùng đi qua một điểm. Giao điểm đó được gọi là trực tâm của tam giác. Thực tế, để tìm tọa độ trực tâm ta không nhất thiết phải vẽ đủ 3 đường cao. Khi vẽ được hai đường cao trong tam giác là bạn đã xác định được trực tâm của tam giác.
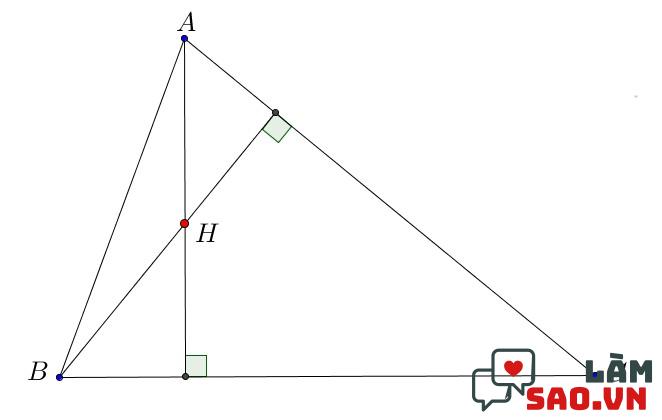
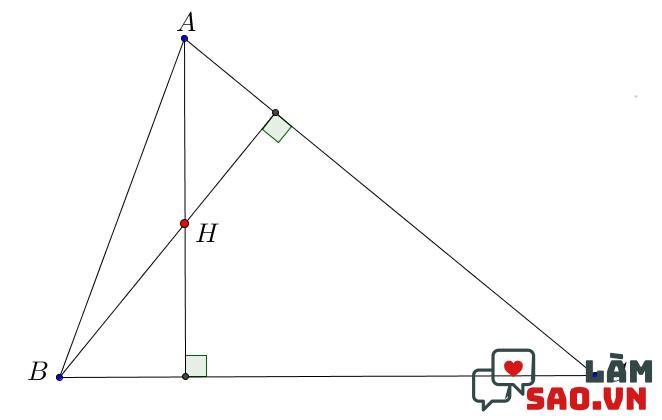
Việc xác định tọa độ trực tâm của tam giác sẽ phụ thuộc vào dạng tam giác. Đối với những dạng tam giác nhọn, tam giác cân, tam giác tù ta cách tìm tọa độ trực tâm đều giống nhau. Từ hai đỉnh của tam giác, lần lượt kẻ các đường cao xuất phát từ đỉnh đến 2 cạnh đối diện. Hai đường đó giao nhau tại điểm nào thì đó chính là trực tâm. Hiển nhiên, khi vẽ đường còn lại đi qua trực tâm đó bạn sẽ thấy nó vuông góc với cạnh còn lại.
Trong trường hợp tìm tọa độ trực tâm là tam giác vuông. Tính chất của tam giác vuông có 2 cạnh vuông góc với nhau tạo thành hai đường cao. Vậy nên, trực tâm tam giác vuông chính là điểm trùng với đỉnh góc vuông.
Những tính chất cần nhớ về trực tâm của tam giác
Dưới đây là các tính chất, các bạn học nhất định cần ghi nhớ để vận dụng linh hoạt cho các bài tập về chứng minh hình học.
- Tính chất 1: Trong tam giác cân, đường trung trực tương ứng cạnh đáy đồng thời là đường trung tuyến, đường phân giác và là đường cao tương ứng đỉnh đối diện với cạnh này.
- Tính chất 2: Trong tam giác, nếu một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
- Tính chất 3: Trong tam giác, nếu một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác cân.
- Tính chất 4: Cho tam giác ABC nhọn, trực tâm tam giác đó sẽ trùng tâm đường tròn nội tiếp tam giác có 3 đỉnh là chân 3 đường cao kẻ từ các đỉnh A, B và C đến các cạnh đối diện tương ứng một đỉnh mà cắt đường tròn ngoại tiếp tại điểm thứ hai sẽ đối xứng trực tâm qua cạnh tương ứng.
Như vậy, ta có hệ quả: Trong một tam giác đều, ta có trọng tâm, trực tâm, điểm cách đều với 3 đỉnh, điểm nằm trong tam giác và cách đều ba cạnh sẽ là 4 điểm trùng nhau.
Muốn học giỏi toán hình, trước tiên các bạn cần là phải nắm vững kiến thức về định nghĩa và các tính chất liên quan. Hy vọng rằng, Lamsao đã giúp bạn đọc hiểu chi tiết về trực tâm là gì? tìm tọa độ trực tâm thế nào? Đừng ngần ngại hãy để lại câu hỏi nếu có vấn đề gì chưa hiểu nhé.